安全多方计算MPC

祈雨的笔记

2025-01-01

other

介绍

隐私计算

随着数字化和大数据分析技术的迅猛发展，对多方数据的需求日益增长。例如，在评估个人信用风险时，需要综合考量多种属性特征，进行联合统计分析，其中需要依赖大量的隐私数据。然而，由于严格的法律法规限制及高昂的数据采集成本，使得数据共享变得困难重重。另外数据本身具备低成本复制性、所有权界定模糊、流通渠道难以控制以及使用范围不易限定等特点，这导致了即使是最微小的安全疏忽也可能引发严重的数据泄露问题。

因此，在确保数据安全与隐私保护的前提下实现征信数据的有效整合成为了一个急需解决的问题。同时，如何确保这些敏感信息在使用过程中的传播是可控的也显得尤为重要。

而隐私计算则是一种旨在保护数据隐私的同时，还能实现数据分析和共享的技术。它通过使用一系列技术手段（如安全多方计算、可信执行环境、联邦学习等），在不暴露原始数据的前提下，完成对数据的处理和分析，从而达到既利用了数据价值又保护了个人或机构隐私的目的。

什么是MPC

安全多方计算（Secure Multi-Party Computation，MPC）允许一个群组的多个参与方在不披露任意参与方私有输人的条件下实现联合计算。参与方约定一个待计算的函数，随后应用MPC协议，将每个人的秘密输入协议中，联合计算得到函数的输出，同时不泄漏私有输入。该技术的特点包括：输入的隐私性、计算的正确性、去中心化。

输入的隐私性：多方安全计算主要是针对在无可信第三方的情况下，能够安全地计算一个约定函数，同时保障协同计算时各用户的隐私数据安全。
计算的正确性：数据在各个节点根据固定的相关逻辑，从本地数据中进行采集并计算，最后将输出的计算结果发送至指定节点，从而多方完成协同计算任务，输出唯一性结果。在保证数据隐私的情况下，将计算结果反馈到整个计算任务系统，从而各方得到正确的数据反馈。
去中心化：在传统分布式计算中，都有中心节点来收集用户信息并进行运算后派发给各个输入方，而多方安全计算协议进行去中心化处理，即保证各参与方权力平等，不存在拥有特权的输入方或者第三方。

简单地讲，MPC主要通过设计特殊的加密算法和协议，基于密码学原理实现在无可信第三方情况下，在多个参与方输入的加密数据之上直接进行计算，期间其他参与方无法解密出己方的加密输入而计算出最终结果。其主要涉及的协议有不经意传输、混淆电路、秘密分享、同态加密等。

MPC密码学协议

MPC还有专用MPC协议和通用MPC协议之分。通用MPC协议如秘密共享、混淆电路等理论上是可以支持任意计算，但是对于某些特定场景，其性能未必高，往往还是需要设计专用的MPC协议才能达到较好的实用性。目前，专用 MPC 协议主要在隐私求交（PSI），隐匿查询（PIR) 领域比较火热，如 PSI 技术当前可以达到十亿级/小时级别的实用性能。

MPC计算需要保证隐私和正确性。在存在对抗行为的情况下，必须保证安全属性。主要考虑两个经典的对手模型：半诚实（半诚实的对手遵循协议规范，但可能会尝试从协议记录中了解更多信息）和恶意（恶意对手可以运行任意攻击策略以试图破坏协议）。另外，如果一个含有多个参与实体的MPC协议中存在不超过一半的参与者可以作出包括合谋在内的不诚实行为，并且协议能保障除计算结果外不会泄露任何参与实体的隐私，则称该MPC协议为诚实大多数，相反超过一半则称为不诚实大多数。

目前，大多数落地的MPC协议还停留在半诚实模型和诚实大多数的前提下，这类MPC技术一般不涉及到同态加密等复杂密码计算，性能会比较好。虽然这类协议的计算相对较快，但是无法抵御大多数参与方的合谋攻击。而能够实现恶意模型和非诚信大多数的协议则一般设计复杂的密码学运算，并且性能远低于前者。

通用协议

不经意传输

描述

不经意传输（Oblivious Transfer, OT）是密码学和隐私计算领域中的一种基本协议，它允许一方（发送方）将信息以一种特殊的方式发送给另一方（接收方），使得接收方只能选择性地获取其中的一部分信息，并且发送方不知道接收方选择了哪部分信息。这种机制在保护数据隐私的同时实现了信息的选择性共享。

简单地讲，该协议涉及到两个参与方：

发送方S，持有多个秘密值{X0,X1,X2,…,Xn}
接收方R，持有一个选择值b∈{0,1,2,…,n}

不经意传输协议允许接收方R得到Xb，但无法得到其他秘密值的任何信息，且发送方S无法得到选择值b。

实现

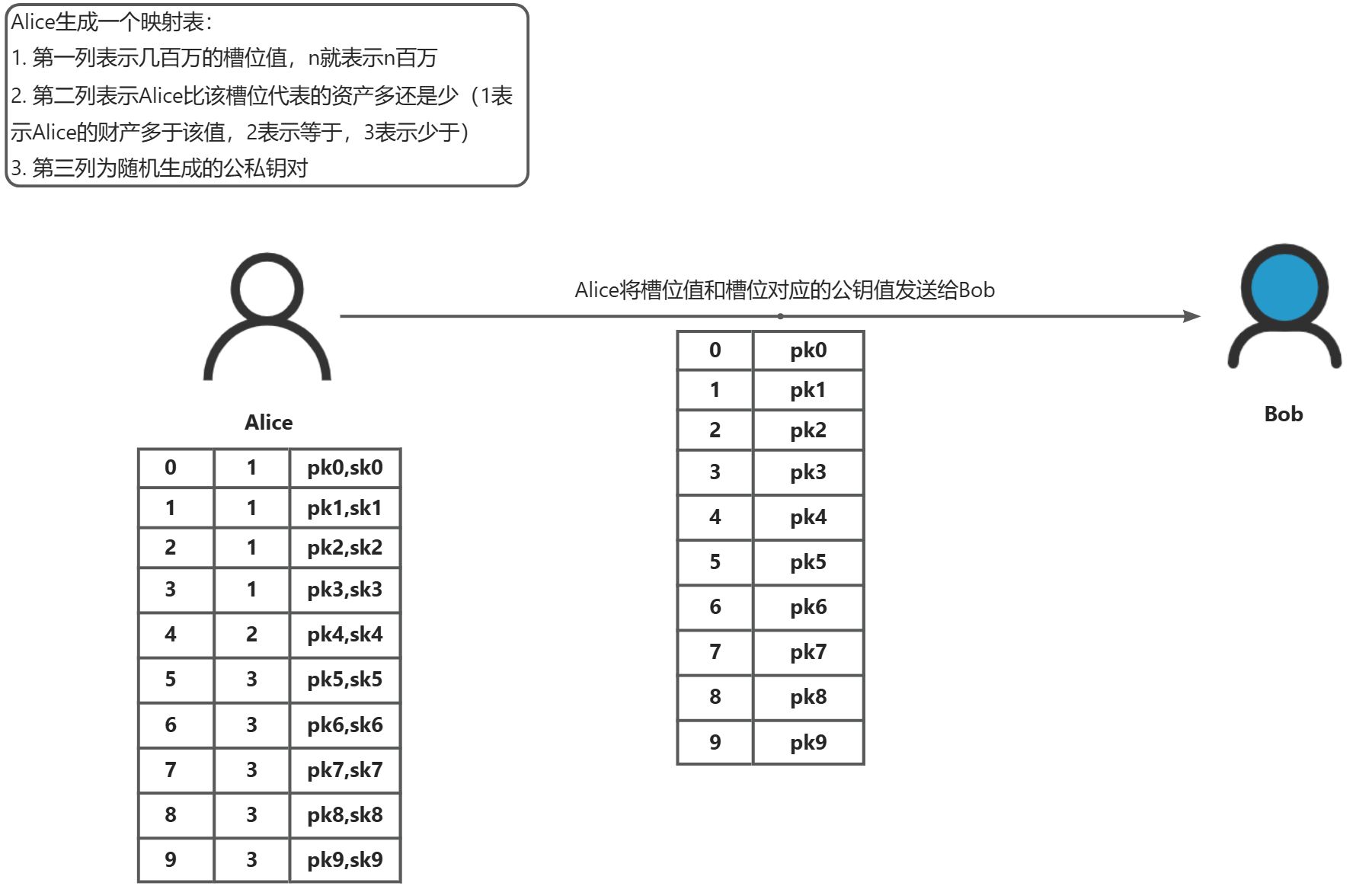
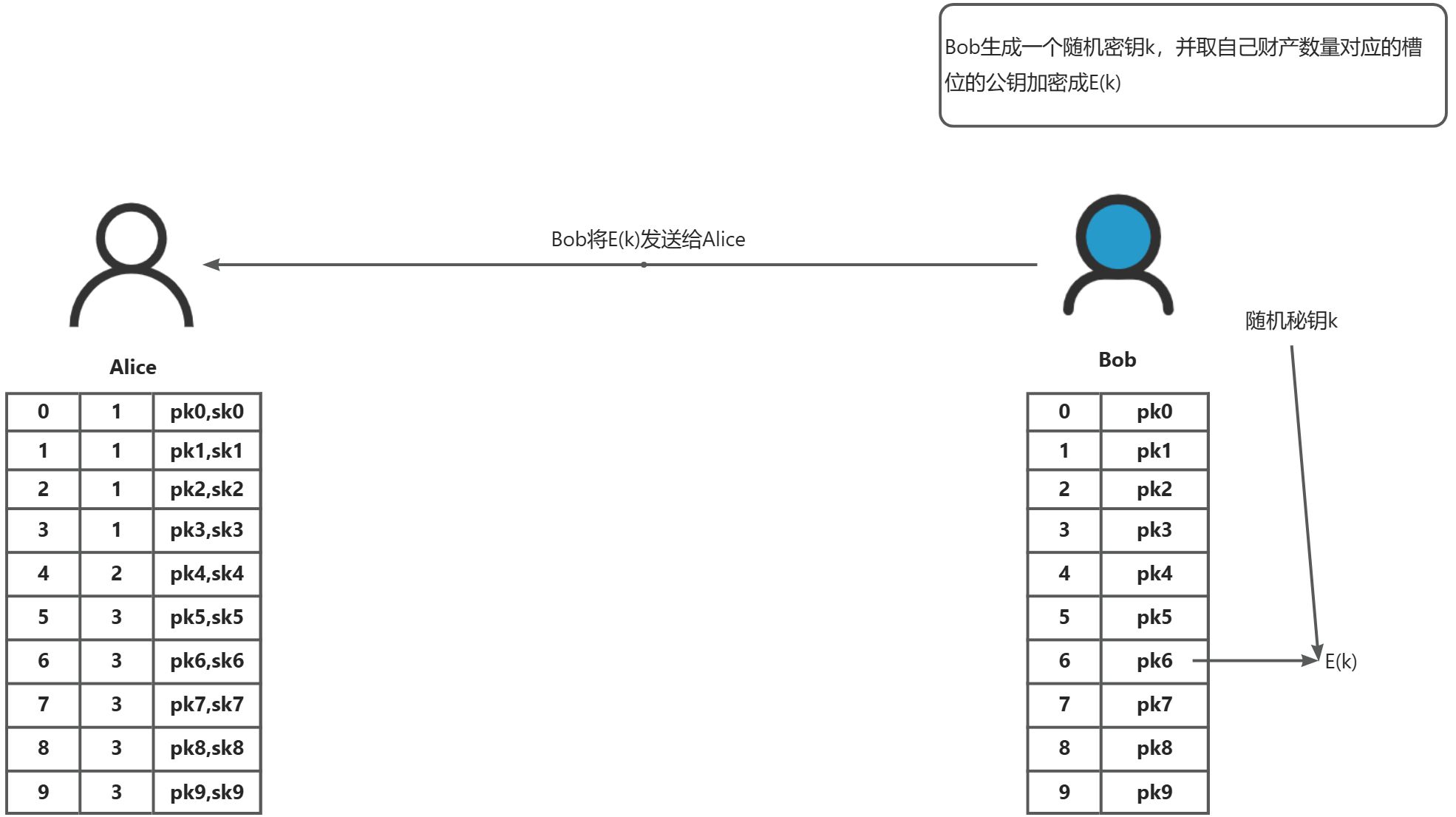
通过经典的百万富翁问题，我们使用一个简单易懂的基于RSA算法实现的OT协议来讲解其中的交互细节

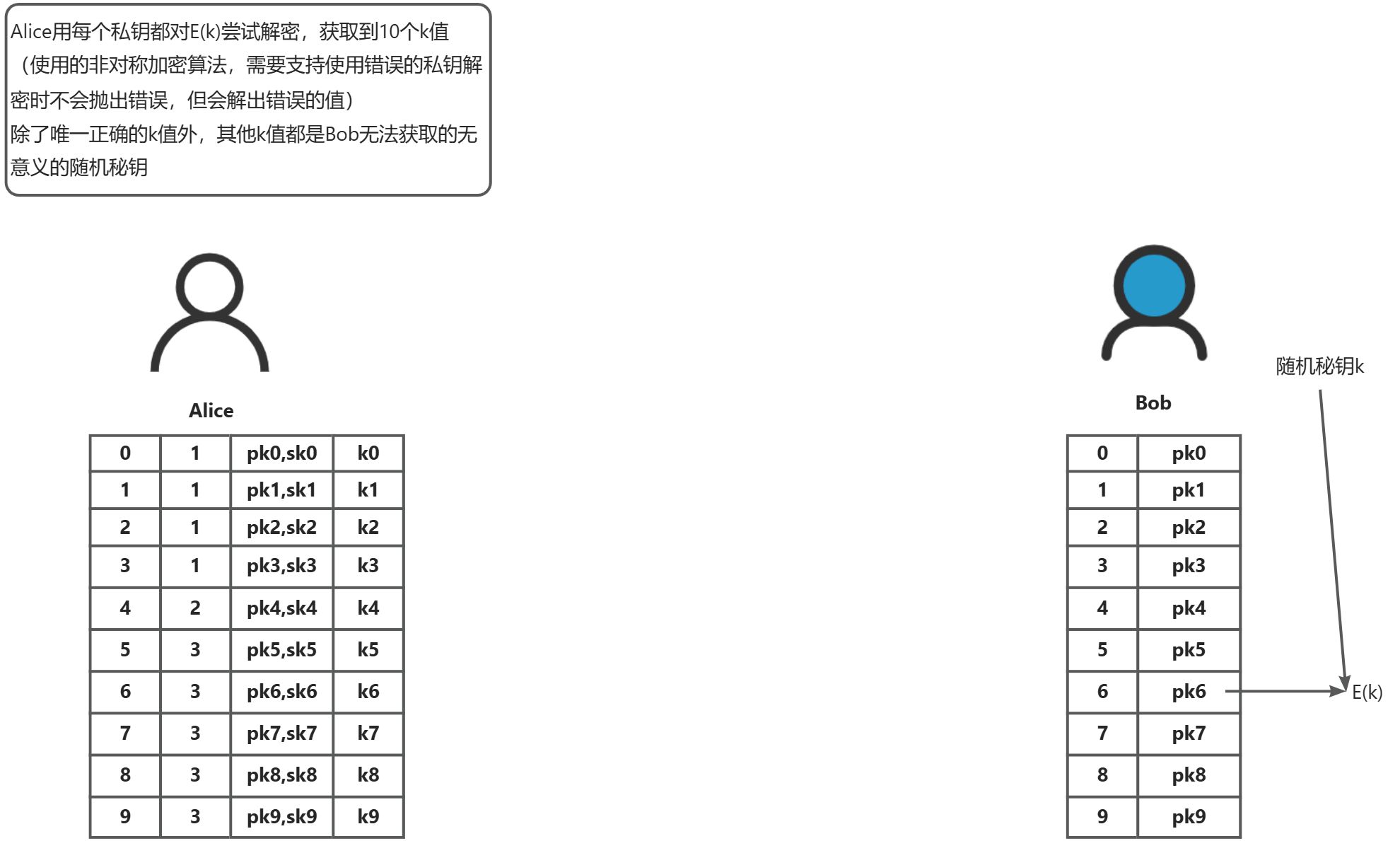
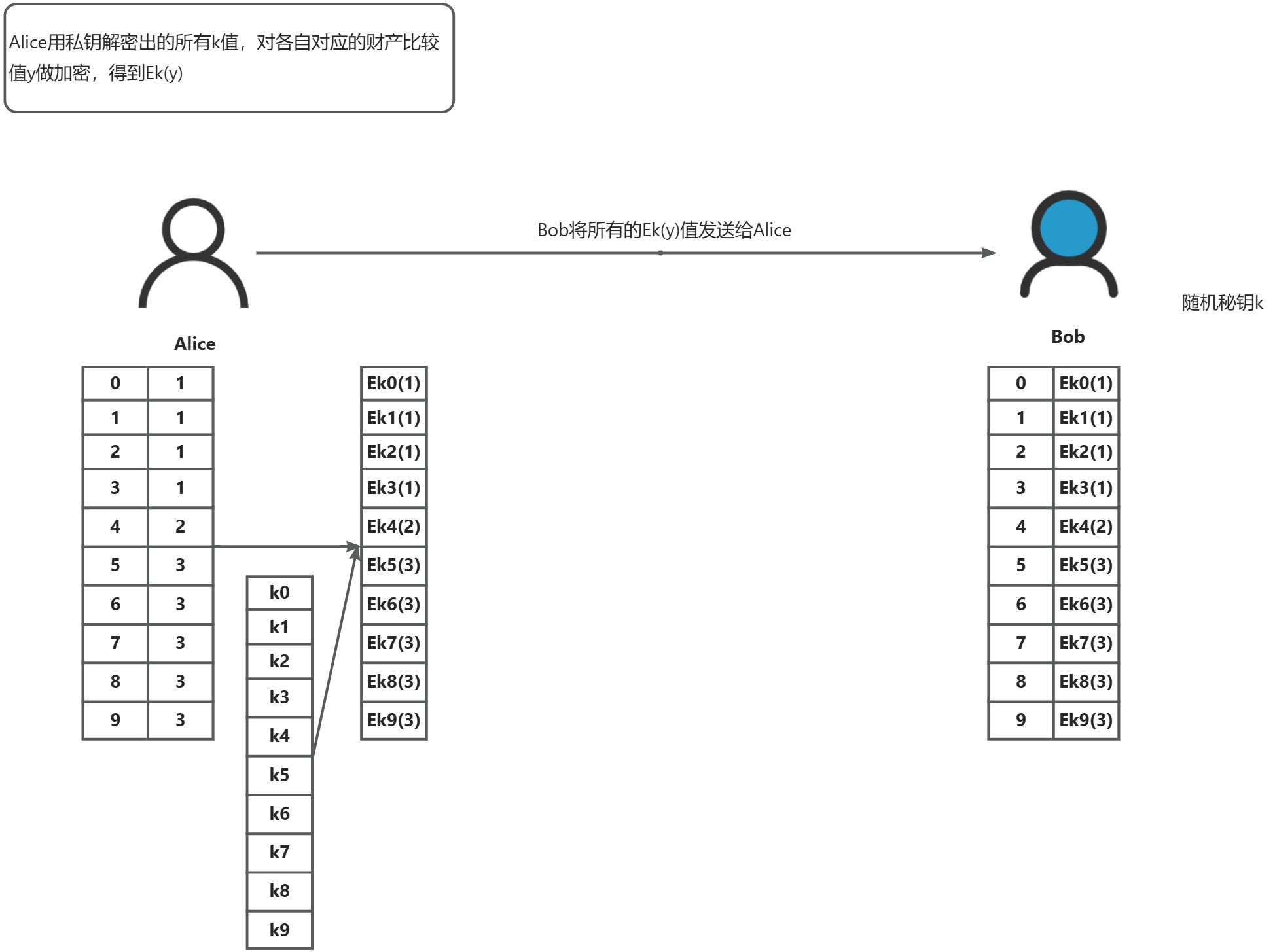
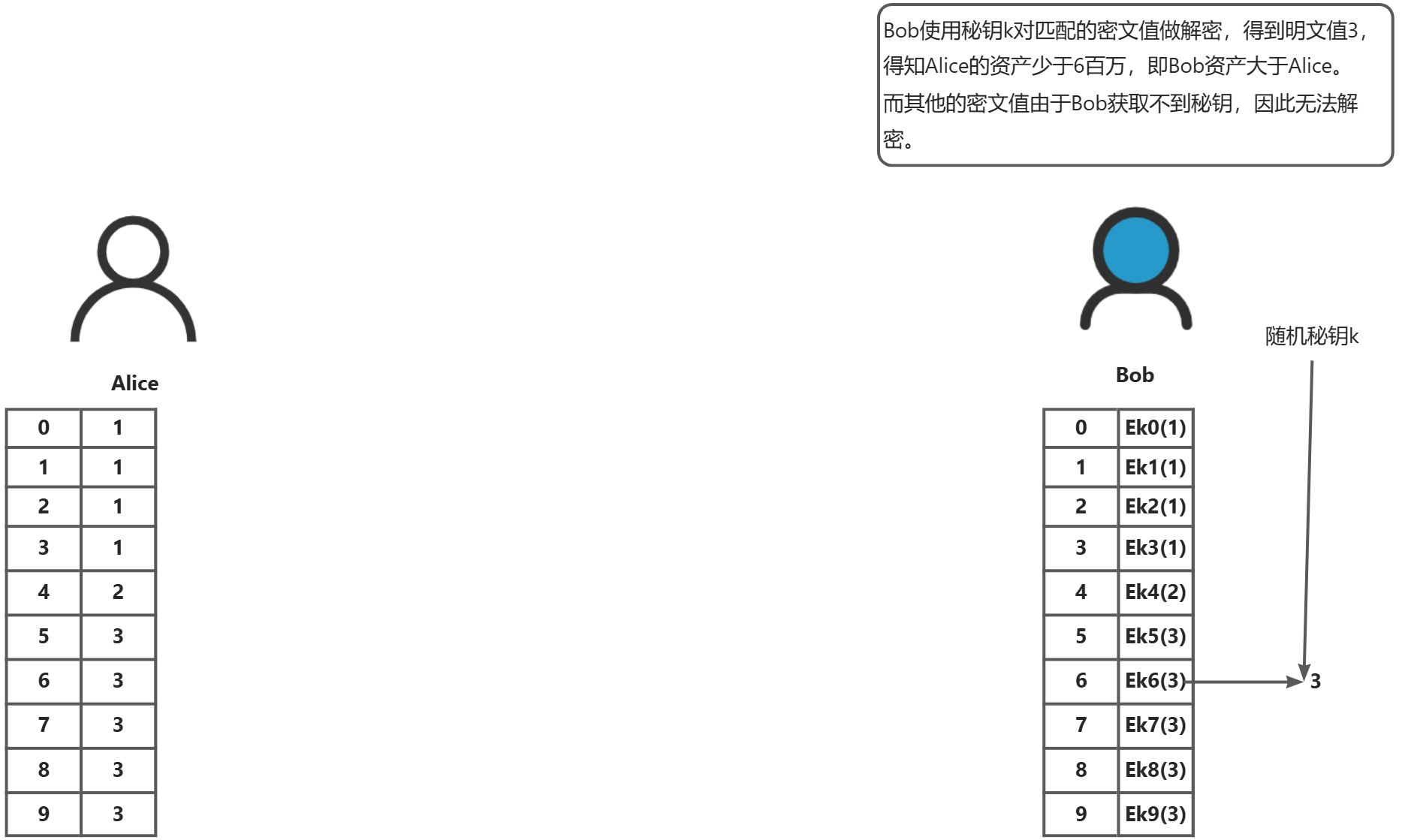
混淆电路

描述

混淆电路（Garbled Circuit, GC）主要用于实现安全的两方或多方位运算。它允许两个或多个参与方在不泄露各自输入的情况下共同完成一个计算任务（该计算任务加密成逻辑电路），并且只获得最终结果，而不会知道对方的具体输入值。这一技术在保护数据隐私的同时实现了有效的信息共享与合作。

在逻辑电路中，与门（AND）、或门（OR）和非门（NOT）被认为是基本的逻辑门。这三种逻辑门单独或者组合起来可以实现任何布尔函数，也就是说，理论上可以通过混淆电路支持任意计算。

实现

下图是一位数的加法电路图，为了简单理解，只抽取其中的与门运算来描述混淆电路的计算过程。

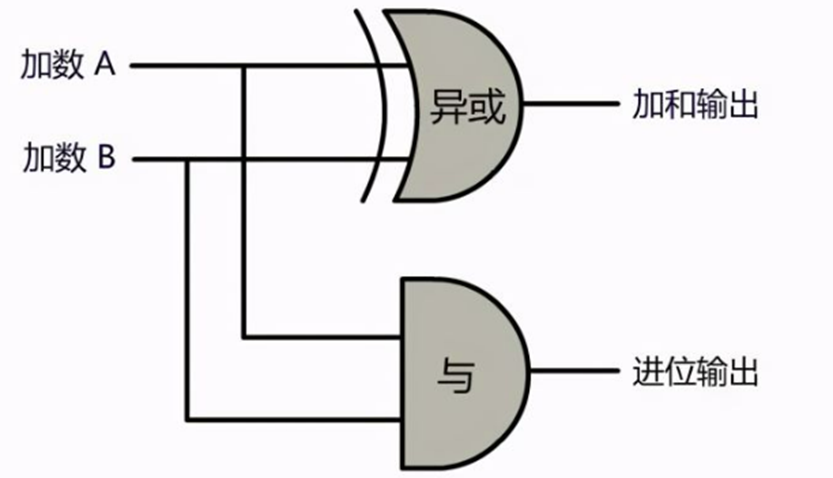
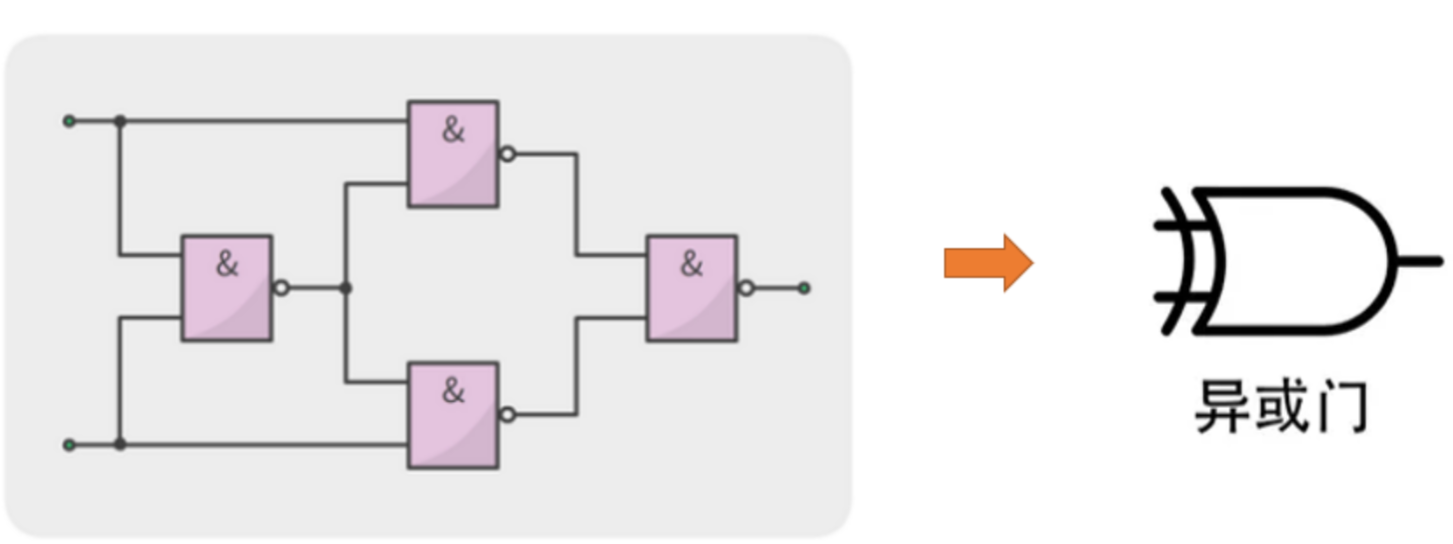
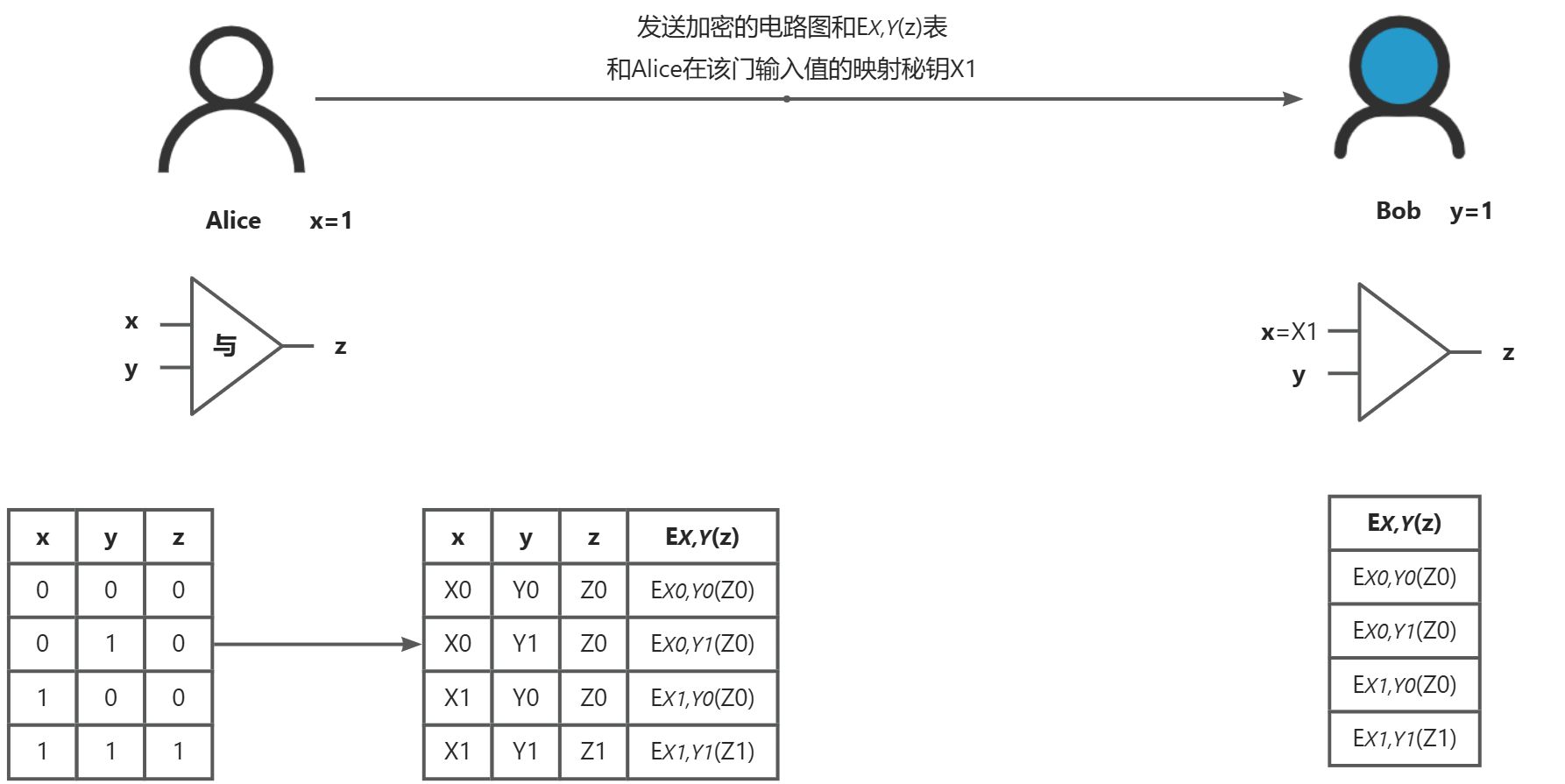
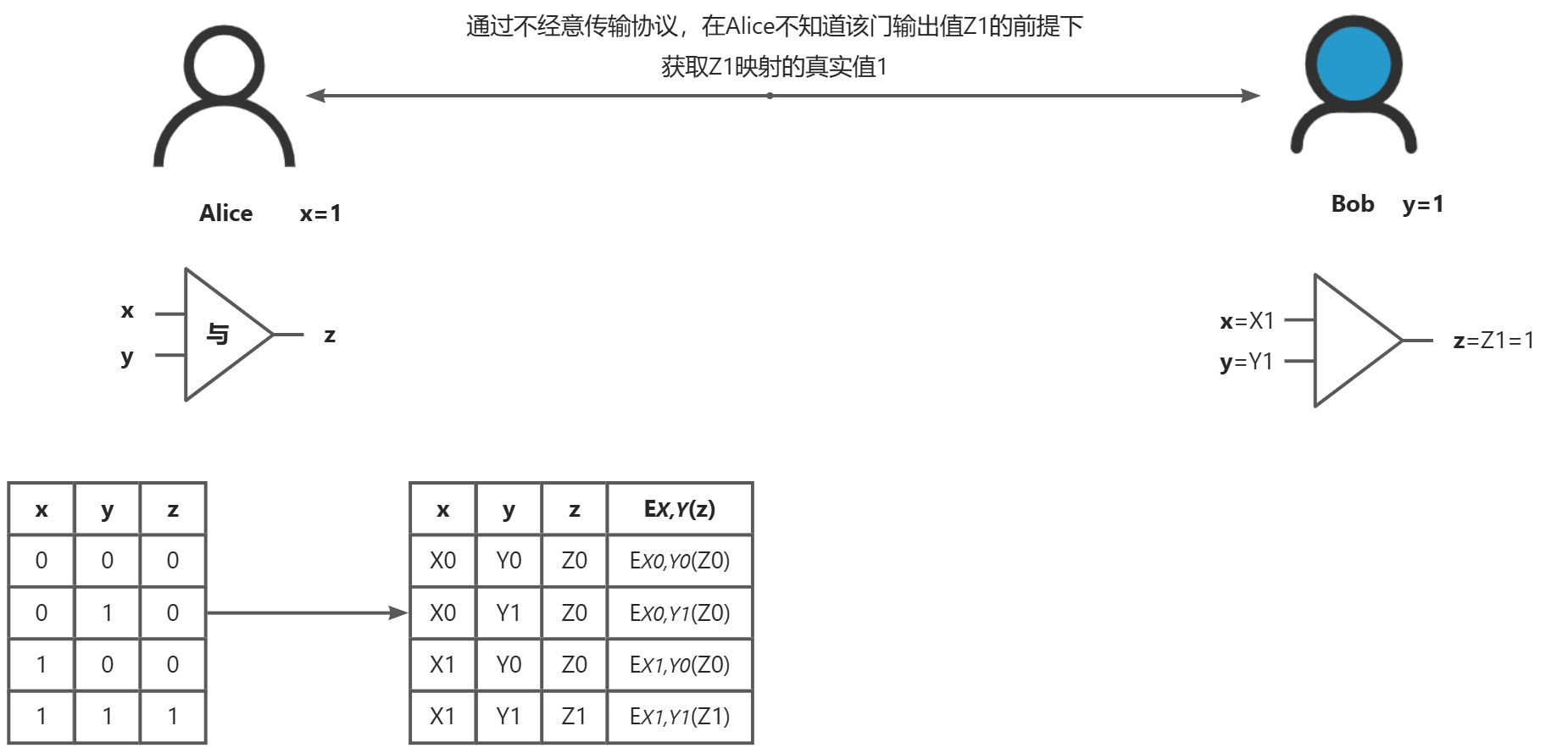
秘密共享

描述

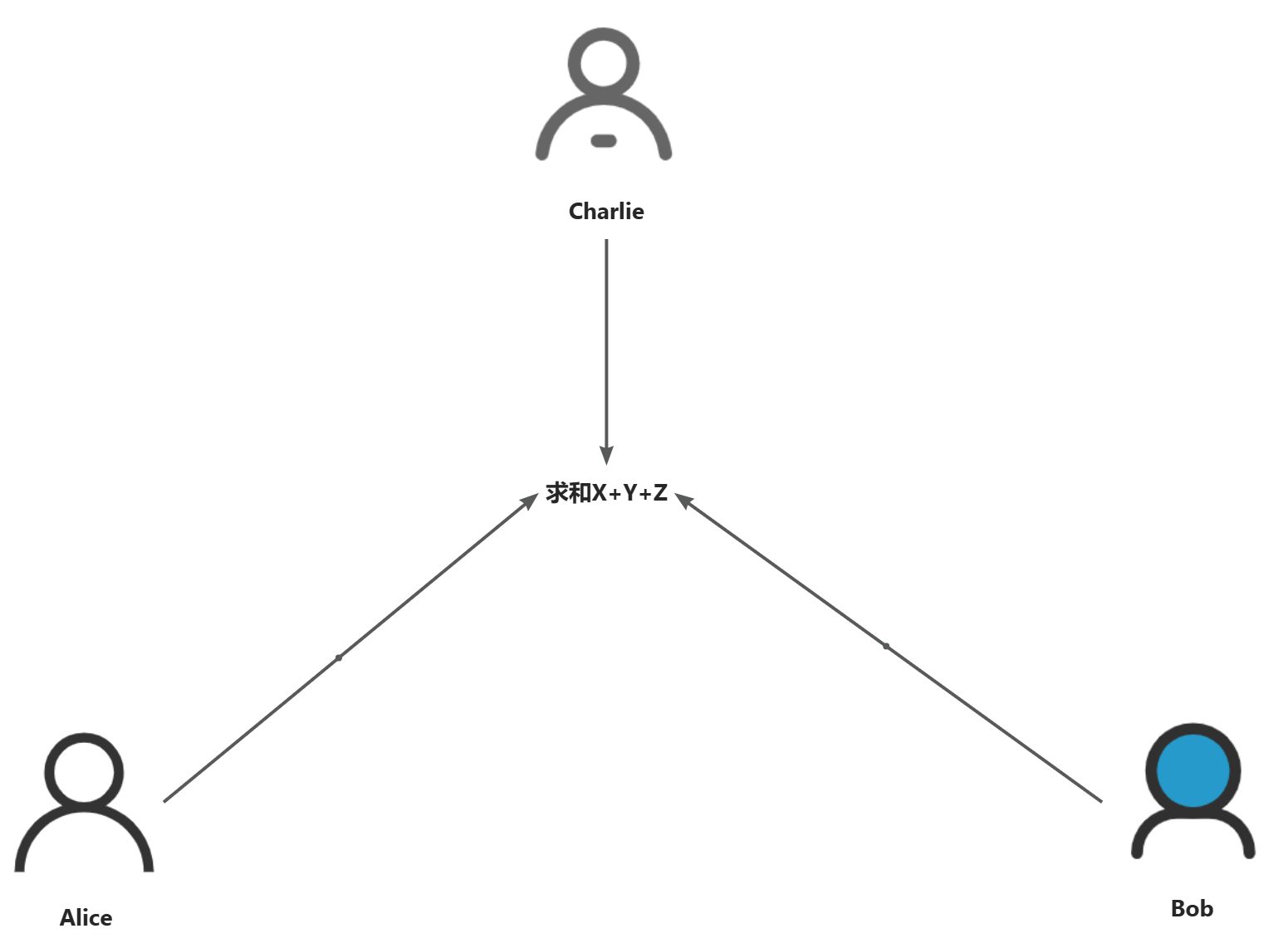
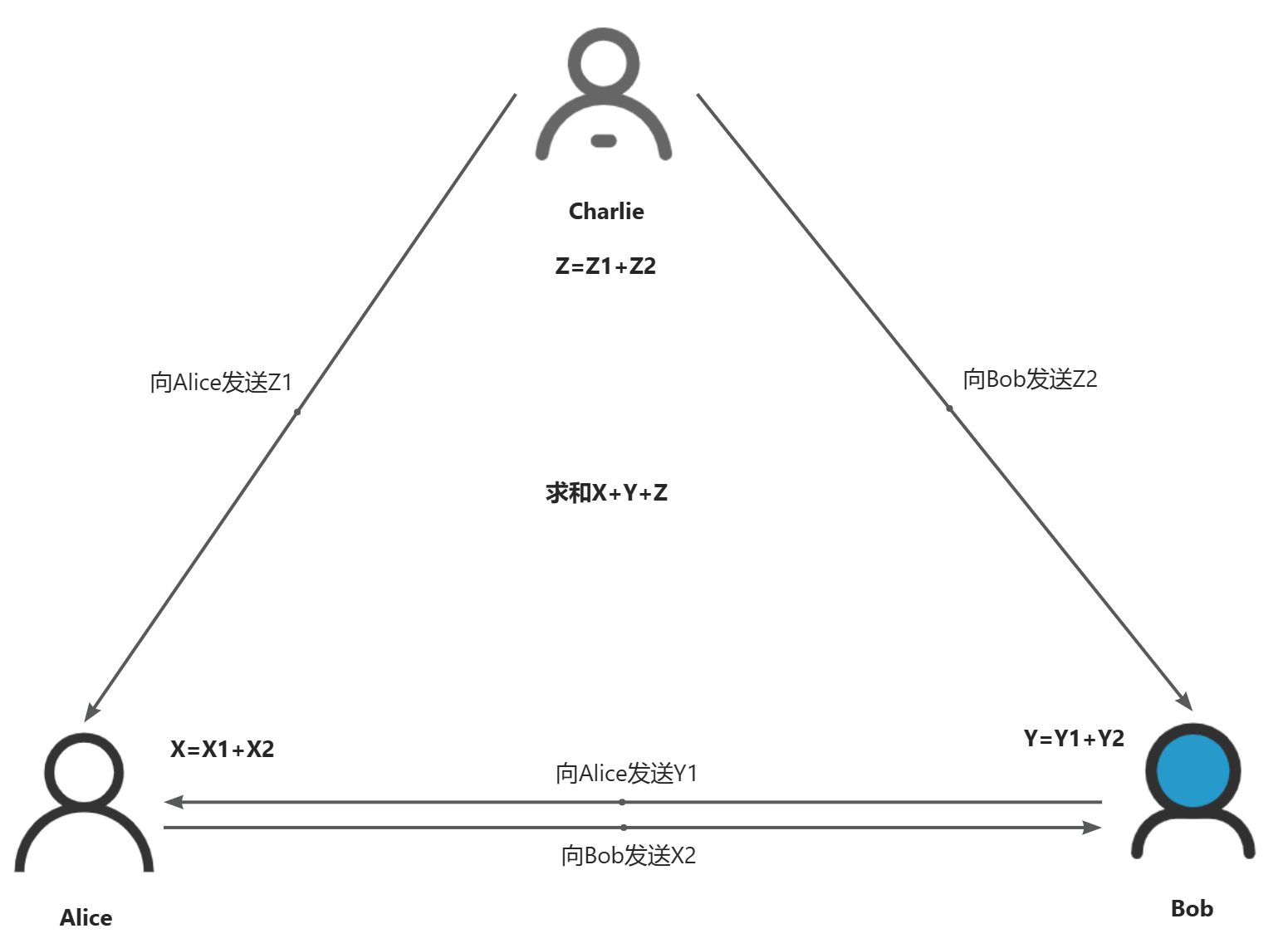
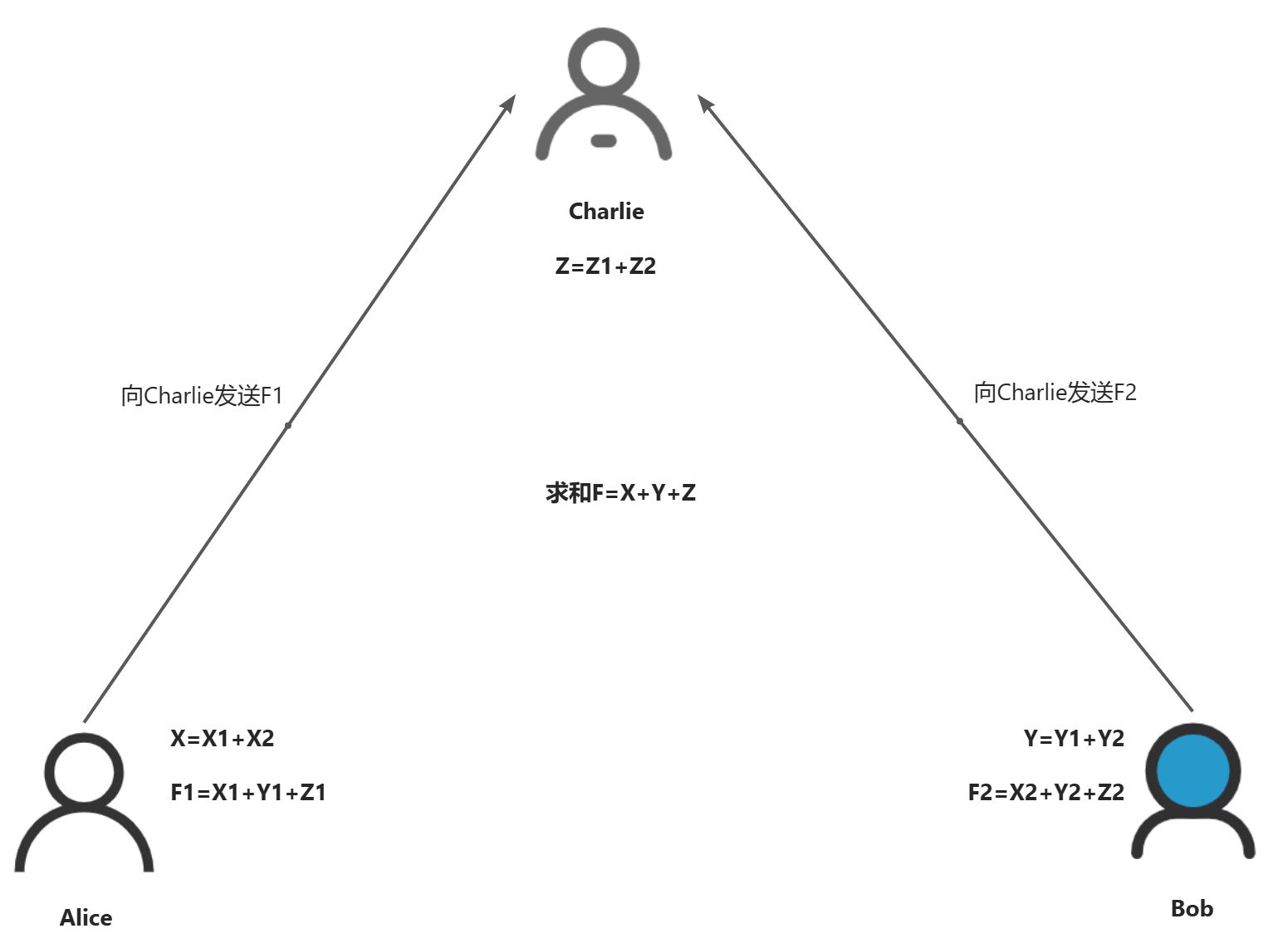
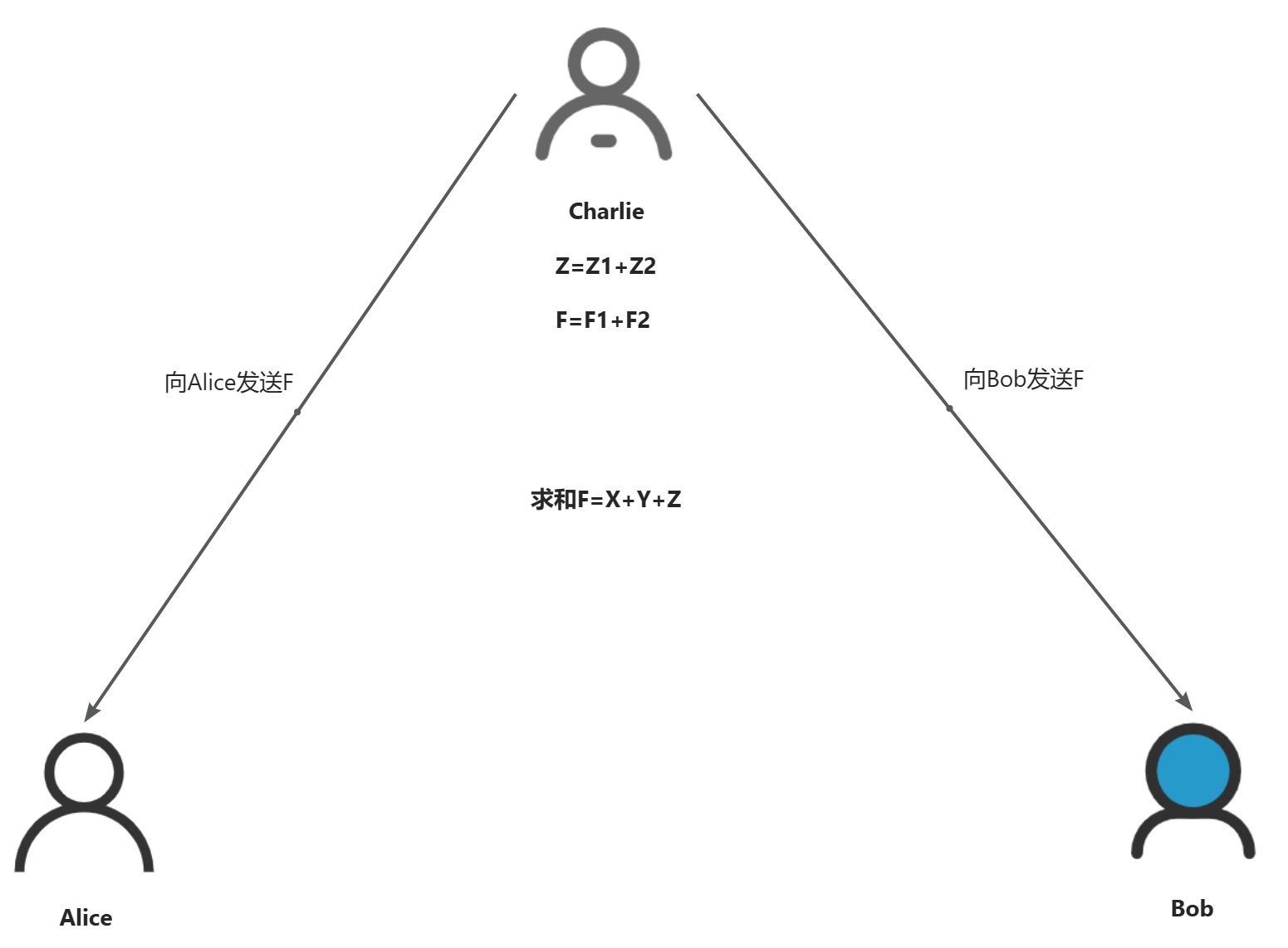
秘密共享（Secret Sharing, SS）允许将一个秘密（如密码、密钥等敏感信息）分割成多个部分，并分配给不同的参与者。这些部分单独来看是没有意义的，只有当满足特定条件下的部分被组合起来时，才能恢复出原始的秘密。这种方法不仅增强了数据的安全性，还支持了多方协作过程中对敏感信息的有效保护。

实现

$ y=f(x)=ax^n + bx^{n-1}+…+c $

n次多项式需要n+1个点，可以求得该方程组有唯一解，从而可以唯一确定多项式的系数。因此可以通过构建n次多项式，将一个常数值y=f(0)构建成需要n+1个分片才能恢复的秘密。

同态加密

同态加密（Homomorphic Encryption, HE）是一种特殊的加密形式，它允许直接对密文进行计算，得到的结果解密后与对原始明文执行相同操作得到的结果一致。这种技术使得数据可以在被加密的状态下进行处理，从而在不泄露数据内容的前提下实现数据的共享和利用。

加法同态：如果一个加密方案支持两个密文相加后解密得到的结果等于这两个密文对应的明文之和，则称该加密方案具有加法同态性，即F(x)+F(y)=F(x+y)。
乘法同态：类似地，如果一个加密方案支持两个密文相乘后解密得到的结果等于这两个密文对应的明文之积，则称其具有乘法同态性，即F(x)F(y)=F(xy)。
全同态加密(Fully Homomorphic Encryption, FHE)：当一个加密系统同时具备加法同态性和乘法同态性时，则称其为全同态加密。

目前虽然全同态加密的通用性更强，但其性能远低于半同态加密（加法同态和乘法同态），因此在许多实际应用中，人们更倾向于选择更加高效、简便且能满足基本需求的半同态加密技术。

秘钥交换

描述

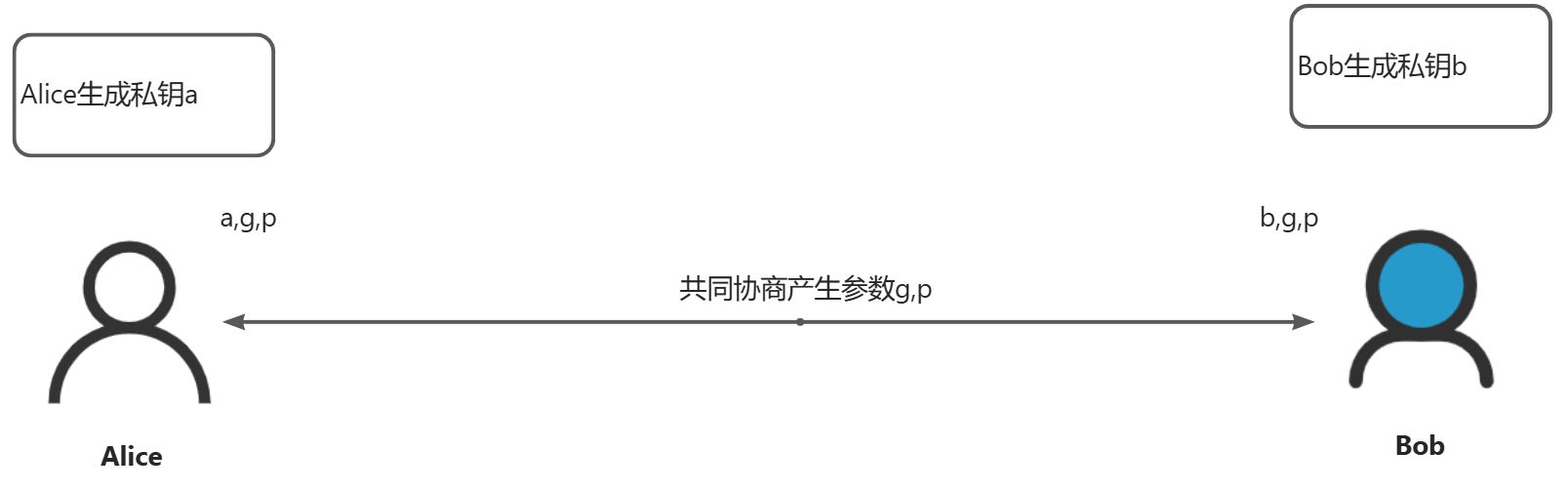
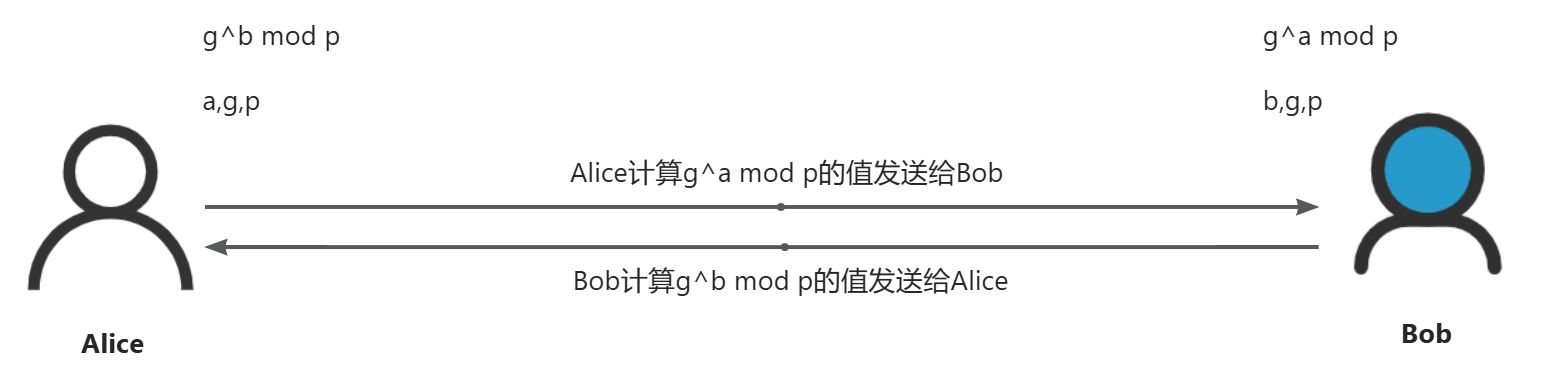
密钥交换（Diffie-Hellman, DH）是一种允许两方在不安全的通信信道上安全地建立共享秘密的方法，它是现代密码学中非常基础且重要的一个组成部分。通过这个过程，双方可以生成相同的密钥，而无需直接传递该密钥本身，从而避免了密钥被中途截获的风险。

实现

$ f_x(g) = g^x\ mod\ p
$

$ f_b(f_a(g)) = f_b(g^a\ mod\ p)=(g^a\ mod\ p)^b\ mod\ p
$

已知$ (g^a\ mod\ p)^b\ mod\ p = (g^b\ mod\ p)^a\ mod\ p $

则$ f_b(f_a(g)) = f_a(f_b(g)) $

专用协议

以上的MPC协议都是基于电路的通用协议。此类协议的网络带宽开销与电路的规模是线性增长关系。对于大规模计算函数，此量级的网络带宽开销是无法承受的。

因此就存在了为特定问题设计专用协议。与通用协议相比，专用协议可以带来巨大的性能提升，但存在一些明显的缺点：

需要设计并证明专用协议的安全性
一般无法将专用协议和通用协议集成到一起。即使存在针对特定函数的高效专用协议，隐私保护应用程序还需要围绕此协议设计额外的预处理或后处理阶段，才能组合使用通用协议和专用协议。在不设计相应转换方案的条件下，一般不可能直接将专用协议和通用协议连接到一起使用
虽然已经存在针对通用协议的安全性增强技术，但可能无法直接（高效地）增强专用协议的安全性，使其经过简单的修改即可抵御恶意攻击

SPI

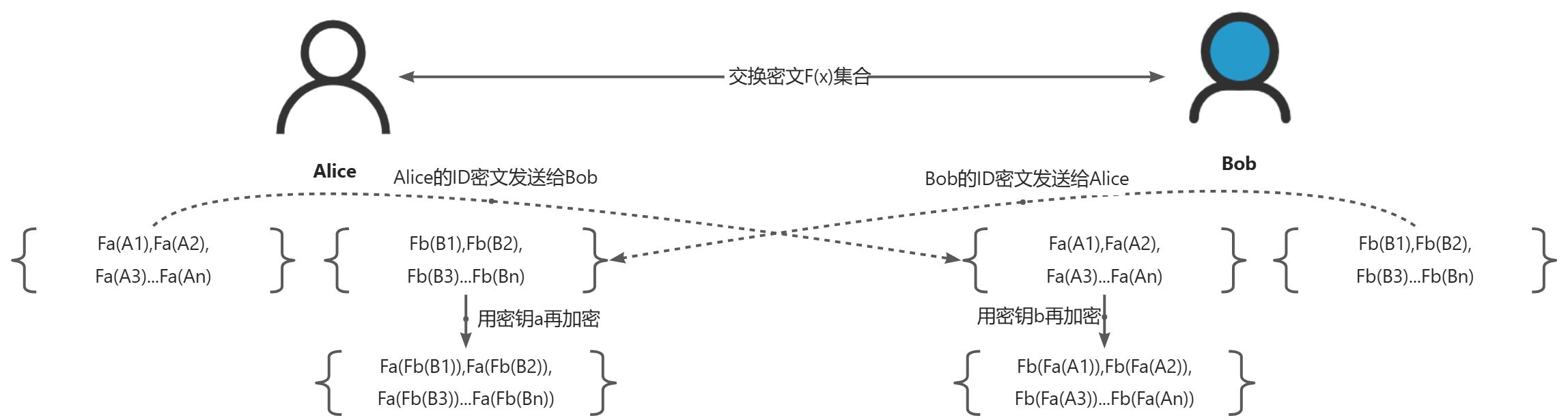
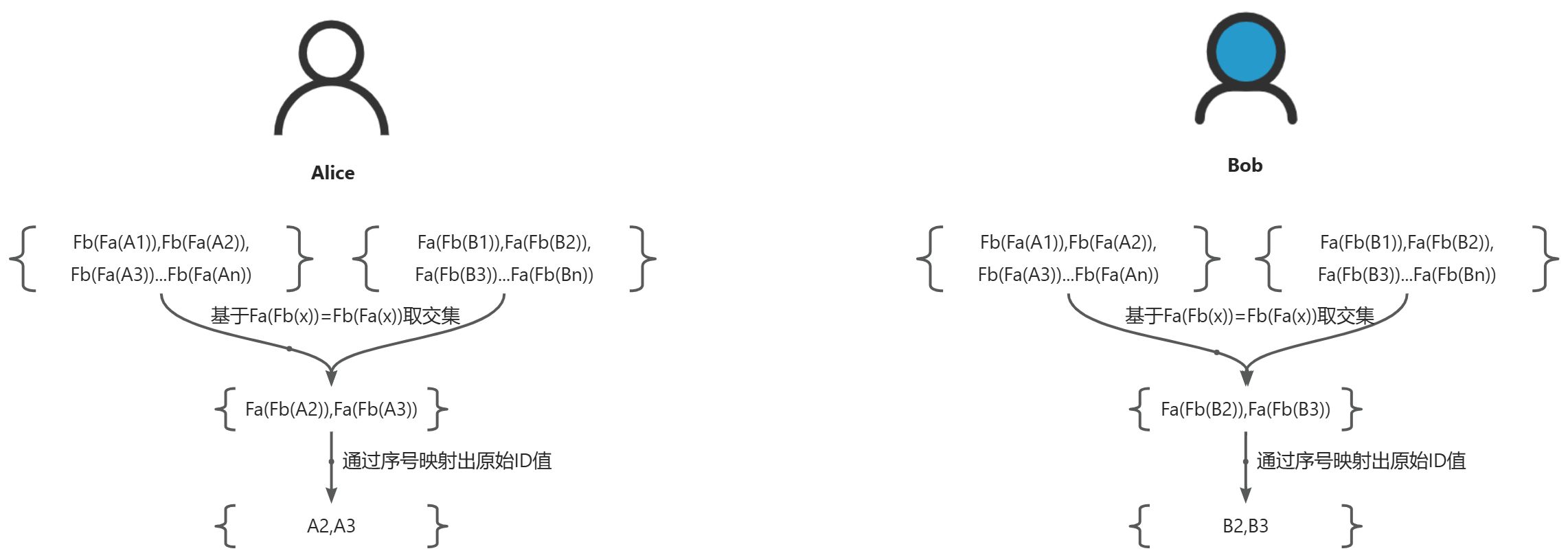
PSI（Private Set Intersection）是一种密码学技术，它允许两个或多个参与方在不泄露各自数据集其他信息的情况下，找出它们之间共同拥有的元素。这项技术对于促进跨组织间的数据合作同时保护用户隐私具有重要意义。

HASH-PSI

在有限输入的场景下，HASH-PSI是不安全的。

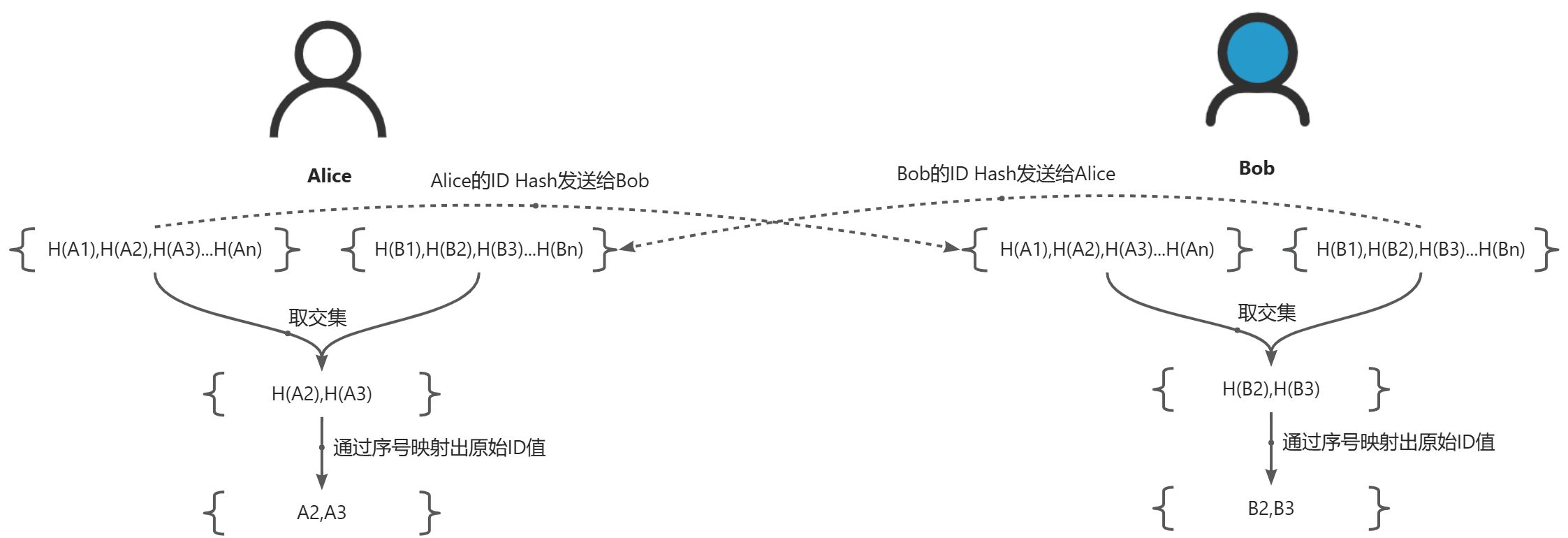
DH-PSI

$ (g^a\ mod\ p)^b\ mod\ p = (g^b\ mod\ p)^a\ mod\ p $

$ f_b(f_a(g)) = f_a(f_b(g)) $